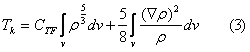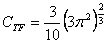45. Logarytm chaotyczny. Sortowanie

    Poprzednio pokazałem, że szereg logarytmiczny dany wzorem 1 zachowuje się chaotycznie dla szeregu wartości zmiennej c :

    Wartości x wypełniają obszar pomiędzy x_min oraz x_max w sposób przypadkowy. Interesowało mnie uporządkowanie tych wartości od największej do najmniejszej. W tym celu do algorytmu generującego szereg chaotyczny dołożyłem prosty algorytm porządkujący (sortujący). Poniżej przedstawiam tekst odpowiedniego programu, który napisałem w języku QBASIC:

'Sortowanie x dla kwadratu funkcji logarytmicznej
'LOG2.BAS
CLS:
x = .7

llos = 10000  'liczba iteracji
DIM wektor(llos)

c = 1.2       'dla c=1.2 min=1.15E-9, max=507.92
OPEN "dywek.txt" FOR APPEND AS #1

FOR i = 1 TO llos
  x = c * LOG(x) ^ 2  'funkcja logarytmiczna
  wektor(i) = x
NEXT i

'sortowanie
FOR j = 1 TO llos - 1
    FOR i = 1 TO llos - 1
      IF wektor(i) > wektor(i + 1) THEN
       tymcz = wektor(i)
       wektor(i) = wektor(i + 1)
       wektor(i + 1) = tymcz
      END IF
    NEXT
NEXT

'zapisywanie danych do pliku tekstowego
FOR i = 1 TO llos
 PRINT #1, wektor(i)
NEXT i
CLOSE #1

    Program generuje plik dywek.txt, w którym zapisane są wartości szeregu od największej do najmniejszej. Wartość największa ma numer 1, a najmniejsza 10000. Rezultat przedstawiłem na poniższym wykresie:

    Otrzymałem wykres funkcji malejącej. Własności tej funkcji nie są dla mnie jasne, ale być może mają jakiś związek z gęstością elektronową. 

44. DFT. Wprawka II. Atom wodoru dokładniej

    Poprzednio pokazałem, że energia stanu podstawowego policzona z sumy dwóch funkcjonałów gęstości (energia Weizsäckera oraz funkcjonał oddziaływania zewnętrznego) prowadzi do zbyt wysokiej wartości tej energii. Obecnie zajmę się poprawkami, które pozwolą na nieco lepsze przybliżenie poszukiwanej wartości. Obliczenia wykonałem na podstawie pracy [1] wraz z zawartymi tam odnośnikami.

    Energia całkowita stanu podstawowego atomu może być przedstawiona za pomocą sumy wkładów energii, będących funkcjonałami gęstości elektronowej (wzór 1):

Gdzie:

T_k - energia kinetyczna elektronu

E_ee  - energia oddziaływania miedzy elektronami (tu równa zero bo jest tylko jeden elektron)

E_xc - energia korelacyjno-wymienna

E_p - energia potencjalna oddziaływania elektron-proton

    Zakładam, że znam postać funkcji gęstości, która jest dana wzorem 2:

    Całkowanie 2 po całej przestrzeni daje wartość 1, co oznacza normalizację gęstości elektronowej do jednego elektronu.  

 
    Wkład energii kinetycznej do całkowitej energii składa się z dwóch elementów (wzór 3). Pierwszy to funkcjonał Thomasa-Fermiego a drugi to funkcjonał von Weizsäckera [2] wzięty ze współczynnikiem 1/5 charakterystycznym dla atomów [3]:

Przy czym:

    Energię korelacyjno-wymienną można rozbić na sumę dwóch funkcjonałów zależnych od gęstości elektronowej w przybliżeniu LDA (Local Density Approximation, wzór 4):

Przy czym potencjał wymienny E_x dany jest wzorem 5:

Natomiast potencjał korelacyjny zbudowany jest z dwóch elementów zależnych od wartości r_s (wzór 6, [4]):

Przy czym (wzór 7):

    Ostatnim elementem jest energia potencjalna elektronu w polu protonu dana wzorem 8:

    W następnym poście pokażę szczegóły obliczeń poszczególnych wkładów energii do energii całkowitej atomu wodoru w stanie podstawowym.

Literatura:

1. H. Chen, A. Zhou, Numer. Math. Theor. Meth. Appl., 2008, 1, 1-28.
2. C. F. von Weizsäcker, Z. Phys., 1935, 96, 431–458.
3. Y. Tomishima, K. Yonei, J. Phys. Soc. Jpn., 1996, 21, 142–153.
4. J. P. Perdew, A. Zunger,  Phys. Rev. B, 1981, 23, 5048–5079.