Poprzednio pokazałem, że energia stanu podstawowego policzona z sumy dwóch funkcjonałów gęstości (energia Weizsäckera oraz funkcjonał oddziaływania zewnętrznego) prowadzi do zbyt wysokiej wartości tej energii. Obecnie zajmę się poprawkami, które pozwolą na nieco lepsze przybliżenie poszukiwanej wartości. Obliczenia wykonałem na podstawie pracy [1] wraz z zawartymi tam odnośnikami.
Energia całkowita stanu podstawowego atomu może być przedstawiona za pomocą sumy wkładów energii, będących funkcjonałami gęstości elektronowej (wzór 1):
Gdzie:
Tk - energia kinetyczna elektronu
Eee - energia oddziaływania miedzy elektronami (tu równa zero bo jest tylko jeden elektron)
Exc - energia korelacyjno-wymienna
Ep - energia potencjalna oddziaływania elektron-proton
Zakładam, że znam postać funkcji gęstości, która jest dana wzorem 2:
Całkowanie 2 po całej przestrzeni daje wartość 1, co oznacza normalizację gęstości elektronowej do jednego elektronu.
Wkład energii kinetycznej do całkowitej energii składa się z dwóch elementów (wzór 3). Pierwszy to funkcjonał Thomasa-Fermiego a drugi to funkcjonał von Weizsäckera [2] wzięty ze współczynnikiem 1/5 charakterystycznym dla atomów [3]:
Przy czym:
Przy czym potencjał wymienny Ex dany jest wzorem 5:
Przy czym (wzór 7):
Ostatnim elementem jest energia potencjalna elektronu w polu protonu dana wzorem 8:
W następnym poście pokażę szczegóły obliczeń poszczególnych wkładów energii do energii całkowitej atomu wodoru w stanie podstawowym.
Literatura:
- H. Chen, A. Zhou, Numer. Math. Theor. Meth. Appl., 2008, 1, 1-28.
- C. F. von Weizsäcker, Z. Phys., 1935, 96, 431–458.
- Y. Tomishima, K. Yonei, J. Phys. Soc. Jpn., 1996, 21, 142–153.
- J. P. Perdew, A. Zunger, Phys. Rev. B, 1981, 23, 5048–5079.
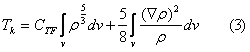
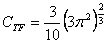
Brak komentarzy :
Prześlij komentarz