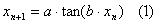47. Chaos w funkcji tangens

Nota autorska

Trudno wchodzić specjalistom w dziedzinę, która nie jest moją profesją naukową. Zdecydowałem zatem, że tu, na moim blogu, opublikuję wyniki dotyczące chaotycznego zachowania się funkcji tangens. All rights reserved.

Zbadano zachowanie chaotyczne funkcji tangens zadanej wzorem iteracyjnym (1)

dla szeregu wartości a oraz pojedynczej wartości b = 1. W tym celu obliczono wykładnini Ljapunowa. Program, który zrealizował to zadanie został napisany w języku VBA for EXCEL:

'Procedura oblicza wykładniki Ljapunowa dla funkcji tangens

Sub Lyapunov()

  N = 10000        'liczba iteracji

  j = 1

  b = 1

  For a = -10 To 10 Step 0.1

    suma = 0

    x = 0.7

    For i = 1 To N

      suma = suma + Log(Abs(a * b * tan(b * x) ^ 2) + 1) 'suma log pochod.

      x = a * tan(b * x)                            'iterowane rown. tangensa

    Next i

    Ljapunow = suma / N    ' wykladnik Lapunowa

    Cells(j, 1) = a

    Cells(j, 2) = Ljapunow

    j = j + 1

  Next a

End Sub

Program zwraca tabelę wielkości, których wykres przedstawiony jest poniżej:

   Dla wartości wykładników Ljapunowa leżących w zakresie lambda <-1 i lambda > 1. Funkcja tangens powinna zachowywać się chaotycznie.

  Zachowanie to przedstawiono za pomocą mapy powrotnej, na której każdy obliczony x_n gra rolę odciętej, a x_n+1 rzędnej:

Sub tangens()

 a = 1.1

 b = 1

 x = 0.7

 For i = 1 To 50000

   y = a * tan(b * x)

   Cells(i, 1) = x

   Cells(i, 2) = y

   x = y

 Next i

End Sub

    Odtwarzany jest dyskretnie przebieg funkcji tangens dla wielu okresów i we wszystkich ćwiartkach układu współrzędnych. Punkty skupione są w pobliżu początku układu. 

    Interesujące jest zbadanie dystrybucji zmiennej chaotycznej w zależności od wartości tej zmiennej. Innymi słowy pokazana zostanie liczebność wystąpienia zmiennej chaotycznej w zależności od wartości tej zmiennej. Obliczenia takie muszą być dokonane na dyskretnym przedziale:

Sub dystrybucja_tangens()

a = 1.1

 b = 1.05

 x = 0.7

 numer = 0

 Range("D1:D1501").ClearContents

 For i = 1 To 1501

   Cells(i, 3) = numer

   numer = numer + 0.01

 Next i

 For i = 1 To 100000

   y = a * tan(b * x)

   If y >= 0 And y <= 15 Then

     numer = Abs(y * 100) + 1

     Cells(numer, 4) = Cells(numer, 4) + 1

   End If

   x = y

 Next i

End Sub

Wynikiem działania programu jest tabela, którą przedstawiono poniżej w postaci graficznej. Na wykresie dystrybucji dodatkowo przedstawiono przebieg funkcji e^-2*x:

    Jak widać dystrybucja funkcji tangens, dla zadanych parametrów i zakresu x od 0 do 15 w dąży do zera sposób regularny. Powstaje pytanie, jaka funkcja najlepiej aproksymuje funkcję chaotycznej dystrybucji tangensa. Być może jest to odpowiednio dopasowana funkcja Gaussa, a może inna.  Wydaje się, że tego typu aproksymacja może mieć znaczenie dla teorii funkcjonałów gęstości, zwłaszcza jeśli zauważymy, że poszerzenie zakresu zbierania danych dystrybucji na wartości ujemne daje stożek, który przypomina stożki gęstości elektronowej, wykorzystywane w analizie Badera do określania punktów charakterystycznych gęstości elektronowej względem wybranej płaszczyzny w związku chemicznym. Poniżej nieznormalizowana dystrybucja w zakresie x od -15 do 15:

Dodatek 18.10.2013. dodaję jeszcze jeden wykres dystrybucji dla funkcji tangens. Uderzające w nim jest to, że bardzo dokładnie przypomina kształtem linię spektralną lampy wodorowej:

46. Nie przyjęli - nie zrozumieli

    Dla kogoś, kto publikuje prace naukowe, odrzucenie pracy przez jakąś redakcję, nie jest niczym niezwykłym. Zdarzyło mi się to cztery razy. Dwukrotnie redakcje, które wydają czasopisma z chemii organicznej miały rację i po niewielkich modyfikacjach tekstu, prace opublikowały inne czasopisma z pożytkiem dla chemii. Zatem rezultat był pozytywny. Trzecie odrzucenie też było słuszne, bo głęboko myliłem się w swoich domniemaniach na temat pewnych aspektów chemii teoretycznej. Tamta pomyłka skutkowała tym, że przestałem się wypowiadać w tej dziedzinie oficjalnie, to znaczy przez publikację w twardych czasopismach. Owszem stosowałem metody chemii kwantowej, jako wspomożenie zrozumienia mechanizmów reakcji, ale to jest rutynowa robota, nie wnosząca do podstaw chemii niczego nowego. Ostatnie odrzucenie jednak pokazało, że dzieje się źle z naszą europejską nauką. Wystarczy opinia kogoś tam, jakiegoś nieznanego nikomu egzaminatora i praca ląduje w koszu. 

    Ciekawe jest to, że trudności powstają, gdy temat jest nowatorski. Trudno ludziom jest go zrozumieć mimo jasnego aparatu matematycznego, który można sprawdzić, przetestować i wyciągnąć wnioski. Jakoś nie chce się dostrzec przez tę zasłonę rutyny, że oto może zdarzyć się coś ciekawego, coś co wywoła lawinę nowych prac, co zmieni fundament wiedzy. Zdaję sobie sprawę, że brzmi to pysznie, ale przez lata byłem "too polite", jak to mi kiedyś powiedział pewien profesor chemii organicznej. Bycie grzecznym w obszarze rutynowej nauki nie przeszkadza, wręcz przeciwnie, pozwala na spokojne publikowanie sensownych wyników. Bycie grzecznym na granicy poznania oznacza ucieczkę przed przyszłością. Ja przestałem być grzecznym. Widzę, że tu trzeba być agresywnym, bo tylko agresja intelektualna może przekonać grzecznych, że kończy się czas wygody, że nadchodzą nowe czasy. Niektórzy nie chcą się zabrać z nowym - ich sprawa - jest tysiące czasopism publikujących szablonowe prace. Ja jednak nie odpuszczę. Fundamenty nauki są dla odważnych. Liczę na to, że wreszcie jakaś kompetentna osoba zrozumie w czym rzecz i zamiast walki o prawdę będzie postęp w ramach metody naukowej.