Przygotowany uprzednio program do obliczania energii stanu podstawowego atomu wodoru z wykorzystaniem metody Monte Carlo i algorytmu Metropolisa zaadaptowałem do obliczenia energii stanu podstawowego cząsteczki H2+. Funkcja falowa, którą wybrałem do obliczeń była kombinacją liniową orbitali 1s atomów wodoru 1:
Parametrem obliczeniowym - odległość między protonami Rj w układzie. Rysunek poniżej przedstawia sytuację geometryczną użytą do obliczeń:
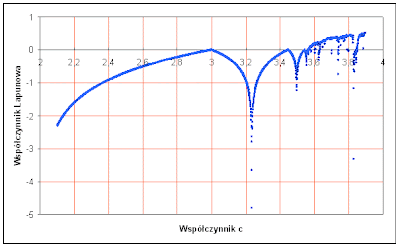
W wyniku przeprowadzonych obliczeń otrzymałem zbiór danych, które są przedstawione na poniższym wykresie:
Wartość minimalna energii wynosi około -0.567 j.at. przy odległości między protonami wynoszącej 2.5 angstrema.
Tekst programu, który wygenerował zbiór wyników jest przytoczony poniżej:
Parametrem obliczeniowym - odległość między protonami Rj w układzie. Rysunek poniżej przedstawia sytuację geometryczną użytą do obliczeń:
W wyniku przeprowadzonych obliczeń otrzymałem zbiór danych, które są przedstawione na poniższym wykresie:
Wartość minimalna energii wynosi około -0.567 j.at. przy odległości między protonami wynoszącej 2.5 angstrema.
Tekst programu, który wygenerował zbiór wyników jest przytoczony poniżej:
DECLARE FUNCTION fufal! (x!, y!, z!)
DECLARE FUNCTION GRNF! () 'gaussowski generator pseudolosowy
'jednostki atomowe
llos = 500000 'liczba losowan
h = .01 'krok rozniczkowania
h2 = h * h 'kwadrat kroku rozniczkowania
DIM SHARED Rj 'odl. miedzy protonami
OPEN "H2plus.txt" FOR APPEND AS #1
FOR Rj = .9 TO 6 STEP .1 'obl. energi w zal. od Rj
En = 0 'zerowanie energii do sumowania
x = 0: y = 1.2: z = 0 'poczatkowy punkt lancucha Markowa
FOR i = 1 TO llos
xzapas = x 'zabezpieczenie starych wspolrzednych
yzapas = y
zzapas = z
psi = fufal(x, y, z) 'wartosc psi w punkcie (x,y,z)
psikw = psi * psi 'kwadrat psi
'Losowanie nowego punktu (xn,yn,zn)
xn = 2 * RND - 1 'zakres (-1, 1)
yn = 2 * RND - 1
zn = 2 * RND - 1
pr = SQR(xn*xn + yn*yn + zn*zn) 'promien punktu (xn,yn,zn)
skok = .6 * GRNF 'skok przypadkowy wg rozkladu Gaussa
x = x + xn * skok / pr 'poprawione wspolrzedne nowego punktu
y = y + yn * skok / pr
z = z + zn * skok / pr
psinowa = fufal(x, y, z) 'wartsc psi w nowym punkcie
psinowakw = psinowa * psinowa
'obliczanie warunku przejscia lancucha do nowego punktu
rel = psinowakw / psikw 'stosunek nowej i starej psi
IF rel < 1 THEN 'przejscie bezwarunkowe gdy rel >= 1
IF RND > rel THEN 'przejscie odrzucone
x = xzapas
y = yzapas
z = zzapas
psinowa = fufal(x, y, z)
END IF
END IF
'obliczanie calki z energii lokalnych
'obliczanie pochodnej w punkcie (x,y,z)
fufal2 = 2 * fufal(x, y, z)
d1 = (fufal(x - h, y, z) - fufal2 + fufal(x + h, y, z)) / h2
d2 = (fufal(x, y - h, z) - fufal2 + fufal(x, y + h, z)) / h2
d3 = (fufal(x, y, z - h) - fufal2 + fufal(x, y, z + h)) / h2
Lappsi = -(d1 + d2 + d3) / 2'druga poch. psi w punkcie (x,y,z)
V1 = -1/(SQR((x - Rj/2)^2 + y*y + z*z))'potencjal psi/psi=1
V2 = -1/(SQR((x + Rj/2)^2 + y*y + z*z))
En = En + Lappsi/psinowa+V1+V2+1/Rj 'suma energii lok.
NEXT i
PRINT #1, Rj, En / llos 'druk zm. wariacyjnej i en. calk.
NEXT Rj
CLOSE #1
END
FUNCTION fufal (x, y, z)
x1 = x - Rj / 2
x2 = x + Rj / 2
r1 = SQR(x1 * x1 + y * y + z * z)
r2 = SQR(x2 * x2 + y * y + z * z)
fufal = EXP(-r1) + EXP(-r2)
END FUNCTION
FUNCTION GRNF
r1 = SQR(-LOG(1 - RND))
GRNF = r1 * SIN(2 * 3.14159265# * RND)
END FUNCTION