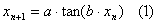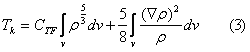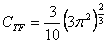50. Właściwości chaotyczne gęstości elektronowej stanu 2s atomu wodoru

Wprowadzenie 
Sam się sobie dziwię, ale kiedyś to napisałem.
    Poprzednio wykazaliśmy, że gęstość elektronowa stanu podstawowego atomu wodoru może być wytworzona poprzez iterację logarytmicznego równania odwrotnego do funkcji gęstości elektronowej tego stanu. Pokazaliśmy, że taka gęstość daje rozmytą chmurę gęstości. Zasadnicza różnica polega na tym, że gęstość "schrödingerowska" rozciąga się od zera do nieskończoności, natomiast gęstość chaotyczna jest ograniczona przestrzennie. Ten wynik powoduje, że gęstość elektronowa jest skupiona w przestrzeni rzędu pojedynczego promienia Bohra.


Chaos gęstości elektronowej stanu 2s atomu wodoru

    W niniejszym szkicu zajmiemy się właściwościami chaotycznymi gęstości elektronowej opartej na nieunormowanej funkcji 2s atomu wodoru (jednostki atomowe). Próbna gęstość elektronowa może być dana elastycznym wzorem (1), przy czym ścisłą wartość gęstości otrzymuje się dla wartości c = 1:

𝛠_2s=(2-cr)²e^-2cr (1)


Wykładniki Lapunowa równania (1) wyliczone dla wartości c  od 0.1 do 5 z krokiem 0.01 są pokazane na rysunku (1):

Rys. Zależność wartości wykładników Ljapunowa od wartości zmiennej wariacyjnej c

    W zakresie tym wszystkie wykładniki mają wartości ujemne. Wartość maksymalna lambda wynosi -0.017 dla c = 0.21. Wartość minimalna wynosi około -18.22 dla c = 0.5. Wynik ten oznacza, że w badanym zakresie gęstość elektronowa stanu 2s zachowuje się w sposób atraktorowy i nie odtwarza krzywej gęstości tego stanu. Co więcej, dla tej wartości  wykładnika Ljapunowa ciąg chaotyczny wartości promienia szybko zmierza do atraktorów o wartości 4 oraz 0, jeśli się wystartuje z pewnego, dość dowolnie wybranego promienia startowego. Należy zwrócić uwagę na fakt, że wartość 4 odpowiada ściśle promieniowi drugiej orbity Bohra.  Jest to wynik dość zaskakujący i musi prowadzić do wniosku, że na gruncie teorii chaosu elektron zachowuje się niezwykle regularnie. Można przyjąć, że gęstość elektronowa tworzy sferę o promieniu 4a₀ ze względu na fakt, że w stanach typu s gęstość ta jest kulisto-symetryczna. Sfera ta nie jest rozmyta, co pozostaje w zasadniczej sprzeczności z zasadą nieoznaczoności Heisenberga i postulatem Borna. Mimo tego wynik ten jest zadziwiający. Można go chyba zinterpretować w ten sposób, że próba wybicia elektronu z jego stanu powoduje szybki doń powrót przez szereg wartości promienia, które są również skwantowane. Nie jest jasne, dlaczego nie dzieje się to w tak dobitny sposób dla wartości c = 1, ale to wymaga zastanowienia. Dla tej wartości mamy również dwie wartości atraktora (0.001363852, 3.983669543). Są to wartości bliskie oczekiwanym (0, 4), ale tylko bliskie.

48. Theoretical investigation of the chaotic electron density in the hydrogen atom

Personal preface:

The work included below I tried to publish in three important journals of the area of theoretical and computational chemistry. My attempts were completely unsuccessful (detailed information on the request). Censors of these journals rejected this work at the first stage of publication process. They gave different reasons. The first answer and the second one were typical: theoretical and computational chemists are not interested in this theme. Okay – disregard. The third one was more important: A study of the hydrogen atom, which is an exactly solvable problem, is not sufficient for the aims and objectives of [here was a journal name].
And then: In the event you develop a paper that goes further and that reports results on more than the hydrogen atom, it may be that such a paper would be suitable for consideration.
These opinions cited above are very important. It seemed to me that hydrogen atom is the obligatory object for new research attempts in the area of physics. It means that theoretical chemistry have to examine this atom initially. What do mean that "hydrogen atom is exactly solvable problem"? It means, we have Schrödinger equation to calculate hydrogen atom properties. My work is about something else. Please, try to understand this. Actually, I found the new description of the density function for hydrogen atom ground state only. It turned out that it is not enough. But the central point of my work is elsewhere. I showed a completely new ability to describe quantum processes in the hydrogen atom. Maybe the work listed below is written in fatal English, maybe arguments are weak but these reasons could not stopped publication. A this moment, I feel exempted from publication this work in an official journal. 

Wojciech Szczepankiewicz

(Employment data were removed because the work is unofficial)

E-mail: Wojciech.Szczepankiewicz@polsl.pl

Abstract: In this paper is presented a new theoretical method for determination of a hydrogen atom electron density at the ground state. A set of chaotic points created by the iteration of a logarithmic function was used to generate an electron density function characterized by the discrete property and limited spatial reach.

Keywords: Hydrogen atom, electron density, Lyapunov exponent, deterministic chaos, logarithmic function, return map


1. Introduction

Deterministic chaos is mainly used in the research of nonlinear dynamical processes for description of classical chaotic processes in the category of quantum mechanics [1-3], Brown motions in a solution [4], dynamics of time dependent hamiltonians [5] or chaotic processes in molecular vibrations [6,7]. These processes were also examined at the excited atoms in external magnetic fields [8]. According to our knowledge, the procedures for generation of deterministic chaos has not been used in the context of the creation of electron density in an atom.

Because the procedures for generation of deterministic chaos return limited number of points in the limited space, remind results of experimental measurements of electron density. For instance, structure determination of chemical compounds by the X-Ray spectroscopy [9] or the discrete electron diffraction picture created at a double slit Young experiment [10-12]. These results can be theoretically generalized in the term of continuous exponential type functions vanishing at infinity by using the wave theory, Schrödinger equation (wave functions) or Density Functional Theories. In other words, continuous and unlimited (with the exception of nodal planes) wave or density functions are mathematical canvas for describing of limited and discrete experimental results. In this work we will show that logarithmic function, associated with the expotential function by the inverse procedure, can simulate electron density of a hydrogen atom ground state. This simulation returns discrete and spatially limited density results. The central point of the following discussion is the chaotic behaviour of iterated logarithmic function characterized by positive values of the Lyapunov exponents [13]. These functions can be plotted on the so called return maps [14].

2. Determination of chaotic electron density

The non-normalized density function of the hydrogen atom ground state is given by the equation (in atomic units)



where ρ – electron density, r – electron radius vector, c – variational constant.

The Lyapunov exponents λ [13], calculated for r (at c <0.001, 4.0>), are less than zero. This means that the iterated equation

(where r_n+1 corresponds to the r_n value on the return map) shows one or more attractors and does not add any significant information concerning the density function. From another side, the logarithmic function given by Eq. (1) is an inverse function of r.

One can construct chaotic functions by the iterative processes starting from an initial r variable value. Unfortunately, the values of the right side of Eq. (1) are negative for ρ > 1. Thus, it is impossible to calculate r values for these ρ ones. However, the introduction of the module to the right side of Eq. (1) resolves this problem. The new Eq. (2) is infinitely iterable and can be used for an identification of the chaotic processes.

Lyapunov exponents λ for Eq. (2), expressed in Fig. 1, are positive for the interval c<0.19,1.35>. It means additionally that Eq. 2 shows the chaotic behavior in the special case for the non-normalized density function (c = 1) and for the normalized one ( c = 1/π).

Figure 1. Lyapunov exponents for logarithmic Eq. 2. Values λ > 0 indicate the chaotic domain of the function.


The return map of Eq. 2 (c = 1) plotted for the 30000 iteration steps (number of choice), shows the discrete set points concentrated near the origin (Fig. 2).

Figure 2. Return map of the logarithmic Eq. 2. Value r_n correspond to a ρ density.

The first step for the electron density function to be recovered, needs the transposition of the axes shown in Fig. 2. We call the new curve expressed in Fig. 3, a pseudo density function ρ’’, because the values ρ’’ > 1 are situated on the positive side of the r axis (Fig. 3). Those values have no physical significance and have to be removed. It is a computational cost that arises because of the application of a module to the iteration procedure of the logarithmic Eq. 2. For example, 5655 points (about 19.8%) are lost for 30000 iteration steps (see supplementary content).

Fig. 3. Return map of the so called pseudo density function ρ’’. Values greater than 1 are nonphysical.

Removing values greater than one from Fig. 3 can characterize the non-normalized density function of the hydrogen atom ground state in atomic units i.e.

  (Fig. 4.)

Fig. 4. The chaotic electron density function of the hydrogen atom ground state.

Since the function on Fig. 4 was created by a chaotic process, we suggest to call it a Chaotic Electron DEnsity function (CEDE for short). This function is a discrete one, its set point being limited by a number of iterations. The domain range r is limited by the r_min > 0 and r_max < INF. Both r_min and r_max depend on the number of the iteration steps. These values change abruptly at the different number of iterations and these changes present an opposite direction i.e. an increase of the number of iterations results in an increase of the r_max value and a decrease of the r_min. The r_min stabilizes over 1.8×10⁷ iterations at the value of 1.38×10^-08 and r_max over 2.1×10⁸ at the value of 9.72 respectively. These values did not change up to 1×10⁹ iterations. However, it is possible that a greater number of iterations will expand these values. (Calculation details and procedures are available from the author upon request)

3. Summary

CEDE of the ground state of the hydrogen atom is discrete and is limited by the minimum and maximum radius vector of the electron. This fact implies a diffuse but a finite size of the atom. For billion iterations maximum radius CEDE exceeds the Bohr radius of the hydrogen atom 9.72 times (see supplementary content). This means that CEDE can interact with the electron densities of adjacent atoms with a non-zero probability.

Assuming that the iteration that creates CEDE is an image of a physical process, the question should be put about the number of iterations since the creation of the atom until a point on the time. The answer to this question is not yet known, but it suggests that the stationary point of an atom is rather a process that occurs with a certain, unknown frequency.

If the stationary state of an atom is treated as a chaotic process of creation of electron density, it is consistent with the Heisenberg uncertainty principle. Chaotic "appearing and disappearing" of the electron around the nucleus at certain points, preventing the definition of the physical path of the electron in three-dimensional space.

Due to the fact that the electron density of the ground state of the hydrogen atom has a spherical symmetry, the values of the angles in a spherical coordinate system can be selected randomly.

The disadvantage of this description is the fact that it is dependent on the scale, which means that, only for a certain range of electron density equation coefficients this equation does behave chaotically. In the example discussed above, this value domain is well expressed by the scale of atomic units.

4. Reference

1. F. Haake, Quantum Signatures of Chaos, Ed. 2, Springer, New York, 2001.

2. M.C. Gutzwiller, Chaos in Classical and Quantum Mechanics in Interdisciplinary Applied mathematics, vol. 1, Springer, Berlin, 1990.

3. E. Ott, Chaos in Dynamical Systems, Cambridge University Press, Cambridge, 1992.

4. V. Villani, Complexity of polypeptide dynamics: chaos, Brownian motion and elasticity in aqueous solution, J. Mol. Struct.: THEOCHEM, 621 (2003) 127-13.]

5. S. Tiwari, R. Ramaswamy, Nosé-Hoover dynamics of a nonintegrable hamiltonian system,
J. Mol. Struct.: THEOCHEM, 361 (1996) 111-116.

6. G. Wu, Nonlinearity and Chaos in Molecular Vibrations, Elsevier, Amsterdam, 2005.

7. P. Wang, G. Wu, Periodic motions due to nonlinearity: the regular vibrational dynamics of chaotic DCN, J. Mol. Struct.: THEOCHEM, 724 (2005) 203-208.

8. P.K. Chattaraj, B. Maiti, Chemical reactivity dynamics and quantum chaos in highly excited hydrogen atoms in an external field: a quantum potential approach, Int. J. Mol. Sci., 3 (2002) 338-359.

9. J. P. Glusker, M. Lewis, M. Rossi, Crystal Structure Analysis for Chemists and Biologists, Wiley-VCH, New York, 1994, p. 131.

10. C. Jönsson, Elektroneninterferenzen an mehreren künstlich hergestellen Feinsplaten, Z. Phys. 161 (1961) 454-474.

11. C. Jönsson, Electron Diffraction at Multiple Slits, Am. J. Phys. 42 (1974) 4-11.

12. A. Tonomura, J. Endo, T. Matsuda, T. Kawasaki, H. Ezawa, Demonstration of single-electron buildup of an interference pattern, Am. J. Phys. 57 ( 1989) 117-120.

13. S. Lynch, Dynamical Systems with Applications Using MATLAB®, Birkhäuser, Boston, 2004, p. 54.

14. Basic Concepts in Nonlinear Dynamics and Chaos. Annual Meeting of the Society for Chaos Theory in Psychology and the Life Sciences Berkeley, 1996, http://www.vanderbilt.edu/AnS/psychology/cogsci/chaos/workshop/Workshop.html (Accessed Apr 18 2013).

47. Chaos w funkcji tangens

Nota autorska

Trudno wchodzić specjalistom w dziedzinę, która nie jest moją profesją naukową. Zdecydowałem zatem, że tu, na moim blogu, opublikuję wyniki dotyczące chaotycznego zachowania się funkcji tangens. All rights reserved.

Zbadano zachowanie chaotyczne funkcji tangens zadanej wzorem iteracyjnym (1)

dla szeregu wartości a oraz pojedynczej wartości b = 1. W tym celu obliczono wykładnini Ljapunowa. Program, który zrealizował to zadanie został napisany w języku VBA for EXCEL:

'Procedura oblicza wykładniki Ljapunowa dla funkcji tangens

Sub Lyapunov()

  N = 10000        'liczba iteracji

  j = 1

  b = 1

  For a = -10 To 10 Step 0.1

    suma = 0

    x = 0.7

    For i = 1 To N

      suma = suma + Log(Abs(a * b * tan(b * x) ^ 2) + 1) 'suma log pochod.

      x = a * tan(b * x)                            'iterowane rown. tangensa

    Next i

    Ljapunow = suma / N    ' wykladnik Lapunowa

    Cells(j, 1) = a

    Cells(j, 2) = Ljapunow

    j = j + 1

  Next a

End Sub

Program zwraca tabelę wielkości, których wykres przedstawiony jest poniżej:

   Dla wartości wykładników Ljapunowa leżących w zakresie lambda <-1 i lambda > 1. Funkcja tangens powinna zachowywać się chaotycznie.

  Zachowanie to przedstawiono za pomocą mapy powrotnej, na której każdy obliczony x_n gra rolę odciętej, a x_n+1 rzędnej:

Sub tangens()

 a = 1.1

 b = 1

 x = 0.7

 For i = 1 To 50000

   y = a * tan(b * x)

   Cells(i, 1) = x

   Cells(i, 2) = y

   x = y

 Next i

End Sub

    Odtwarzany jest dyskretnie przebieg funkcji tangens dla wielu okresów i we wszystkich ćwiartkach układu współrzędnych. Punkty skupione są w pobliżu początku układu. 

    Interesujące jest zbadanie dystrybucji zmiennej chaotycznej w zależności od wartości tej zmiennej. Innymi słowy pokazana zostanie liczebność wystąpienia zmiennej chaotycznej w zależności od wartości tej zmiennej. Obliczenia takie muszą być dokonane na dyskretnym przedziale:

Sub dystrybucja_tangens()

a = 1.1

 b = 1.05

 x = 0.7

 numer = 0

 Range("D1:D1501").ClearContents

 For i = 1 To 1501

   Cells(i, 3) = numer

   numer = numer + 0.01

 Next i

 For i = 1 To 100000

   y = a * tan(b * x)

   If y >= 0 And y <= 15 Then

     numer = Abs(y * 100) + 1

     Cells(numer, 4) = Cells(numer, 4) + 1

   End If

   x = y

 Next i

End Sub

Wynikiem działania programu jest tabela, którą przedstawiono poniżej w postaci graficznej. Na wykresie dystrybucji dodatkowo przedstawiono przebieg funkcji e^-2*x:

    Jak widać dystrybucja funkcji tangens, dla zadanych parametrów i zakresu x od 0 do 15 w dąży do zera sposób regularny. Powstaje pytanie, jaka funkcja najlepiej aproksymuje funkcję chaotycznej dystrybucji tangensa. Być może jest to odpowiednio dopasowana funkcja Gaussa, a może inna.  Wydaje się, że tego typu aproksymacja może mieć znaczenie dla teorii funkcjonałów gęstości, zwłaszcza jeśli zauważymy, że poszerzenie zakresu zbierania danych dystrybucji na wartości ujemne daje stożek, który przypomina stożki gęstości elektronowej, wykorzystywane w analizie Badera do określania punktów charakterystycznych gęstości elektronowej względem wybranej płaszczyzny w związku chemicznym. Poniżej nieznormalizowana dystrybucja w zakresie x od -15 do 15:

Dodatek 18.10.2013. dodaję jeszcze jeden wykres dystrybucji dla funkcji tangens. Uderzające w nim jest to, że bardzo dokładnie przypomina kształtem linię spektralną lampy wodorowej:

46. Nie przyjęli - nie zrozumieli

    Dla kogoś, kto publikuje prace naukowe, odrzucenie pracy przez jakąś redakcję, nie jest niczym niezwykłym. Zdarzyło mi się to cztery razy. Dwukrotnie redakcje, które wydają czasopisma z chemii organicznej miały rację i po niewielkich modyfikacjach tekstu, prace opublikowały inne czasopisma z pożytkiem dla chemii. Zatem rezultat był pozytywny. Trzecie odrzucenie też było słuszne, bo głęboko myliłem się w swoich domniemaniach na temat pewnych aspektów chemii teoretycznej. Tamta pomyłka skutkowała tym, że przestałem się wypowiadać w tej dziedzinie oficjalnie, to znaczy przez publikację w twardych czasopismach. Owszem stosowałem metody chemii kwantowej, jako wspomożenie zrozumienia mechanizmów reakcji, ale to jest rutynowa robota, nie wnosząca do podstaw chemii niczego nowego. Ostatnie odrzucenie jednak pokazało, że dzieje się źle z naszą europejską nauką. Wystarczy opinia kogoś tam, jakiegoś nieznanego nikomu egzaminatora i praca ląduje w koszu. 

    Ciekawe jest to, że trudności powstają, gdy temat jest nowatorski. Trudno ludziom jest go zrozumieć mimo jasnego aparatu matematycznego, który można sprawdzić, przetestować i wyciągnąć wnioski. Jakoś nie chce się dostrzec przez tę zasłonę rutyny, że oto może zdarzyć się coś ciekawego, coś co wywoła lawinę nowych prac, co zmieni fundament wiedzy. Zdaję sobie sprawę, że brzmi to pysznie, ale przez lata byłem "too polite", jak to mi kiedyś powiedział pewien profesor chemii organicznej. Bycie grzecznym w obszarze rutynowej nauki nie przeszkadza, wręcz przeciwnie, pozwala na spokojne publikowanie sensownych wyników. Bycie grzecznym na granicy poznania oznacza ucieczkę przed przyszłością. Ja przestałem być grzecznym. Widzę, że tu trzeba być agresywnym, bo tylko agresja intelektualna może przekonać grzecznych, że kończy się czas wygody, że nadchodzą nowe czasy. Niektórzy nie chcą się zabrać z nowym - ich sprawa - jest tysiące czasopism publikujących szablonowe prace. Ja jednak nie odpuszczę. Fundamenty nauki są dla odważnych. Liczę na to, że wreszcie jakaś kompetentna osoba zrozumie w czym rzecz i zamiast walki o prawdę będzie postęp w ramach metody naukowej. 

45. Logarytm chaotyczny. Sortowanie

    Poprzednio pokazałem, że szereg logarytmiczny dany wzorem 1 zachowuje się chaotycznie dla szeregu wartości zmiennej c :

    Wartości x wypełniają obszar pomiędzy x_min oraz x_max w sposób przypadkowy. Interesowało mnie uporządkowanie tych wartości od największej do najmniejszej. W tym celu do algorytmu generującego szereg chaotyczny dołożyłem prosty algorytm porządkujący (sortujący). Poniżej przedstawiam tekst odpowiedniego programu, który napisałem w języku QBASIC:

'Sortowanie x dla kwadratu funkcji logarytmicznej
'LOG2.BAS
CLS:
x = .7

llos = 10000  'liczba iteracji
DIM wektor(llos)

c = 1.2       'dla c=1.2 min=1.15E-9, max=507.92
OPEN "dywek.txt" FOR APPEND AS #1

FOR i = 1 TO llos
  x = c * LOG(x) ^ 2  'funkcja logarytmiczna
  wektor(i) = x
NEXT i

'sortowanie
FOR j = 1 TO llos - 1
    FOR i = 1 TO llos - 1
      IF wektor(i) > wektor(i + 1) THEN
       tymcz = wektor(i)
       wektor(i) = wektor(i + 1)
       wektor(i + 1) = tymcz
      END IF
    NEXT
NEXT

'zapisywanie danych do pliku tekstowego
FOR i = 1 TO llos
 PRINT #1, wektor(i)
NEXT i
CLOSE #1

    Program generuje plik dywek.txt, w którym zapisane są wartości szeregu od największej do najmniejszej. Wartość największa ma numer 1, a najmniejsza 10000. Rezultat przedstawiłem na poniższym wykresie:

    Otrzymałem wykres funkcji malejącej. Własności tej funkcji nie są dla mnie jasne, ale być może mają jakiś związek z gęstością elektronową. 

44. DFT. Wprawka II. Atom wodoru dokładniej

    Poprzednio pokazałem, że energia stanu podstawowego policzona z sumy dwóch funkcjonałów gęstości (energia Weizsäckera oraz funkcjonał oddziaływania zewnętrznego) prowadzi do zbyt wysokiej wartości tej energii. Obecnie zajmę się poprawkami, które pozwolą na nieco lepsze przybliżenie poszukiwanej wartości. Obliczenia wykonałem na podstawie pracy [1] wraz z zawartymi tam odnośnikami.

    Energia całkowita stanu podstawowego atomu może być przedstawiona za pomocą sumy wkładów energii, będących funkcjonałami gęstości elektronowej (wzór 1):

Gdzie:

T_k - energia kinetyczna elektronu

E_ee  - energia oddziaływania miedzy elektronami (tu równa zero bo jest tylko jeden elektron)

E_xc - energia korelacyjno-wymienna

E_p - energia potencjalna oddziaływania elektron-proton

    Zakładam, że znam postać funkcji gęstości, która jest dana wzorem 2:

    Całkowanie 2 po całej przestrzeni daje wartość 1, co oznacza normalizację gęstości elektronowej do jednego elektronu.  

 
    Wkład energii kinetycznej do całkowitej energii składa się z dwóch elementów (wzór 3). Pierwszy to funkcjonał Thomasa-Fermiego a drugi to funkcjonał von Weizsäckera [2] wzięty ze współczynnikiem 1/5 charakterystycznym dla atomów [3]:

Przy czym:

    Energię korelacyjno-wymienną można rozbić na sumę dwóch funkcjonałów zależnych od gęstości elektronowej w przybliżeniu LDA (Local Density Approximation, wzór 4):

Przy czym potencjał wymienny E_x dany jest wzorem 5:

Natomiast potencjał korelacyjny zbudowany jest z dwóch elementów zależnych od wartości r_s (wzór 6, [4]):

Przy czym (wzór 7):

    Ostatnim elementem jest energia potencjalna elektronu w polu protonu dana wzorem 8:

    W następnym poście pokażę szczegóły obliczeń poszczególnych wkładów energii do energii całkowitej atomu wodoru w stanie podstawowym.

Literatura:

1. H. Chen, A. Zhou, Numer. Math. Theor. Meth. Appl., 2008, 1, 1-28.
2. C. F. von Weizsäcker, Z. Phys., 1935, 96, 431–458.
3. Y. Tomishima, K. Yonei, J. Phys. Soc. Jpn., 1996, 21, 142–153.
4. J. P. Perdew, A. Zunger,  Phys. Rev. B, 1981, 23, 5048–5079.

43. DFT. Wprawka I. Energia stanu podstawowego atomu wodoru z funkcjonału Weizsäckera

    W książce [1] znajduje się wyprowadzenie energii stanu podstawowego atomu wodoru i jonu H₂+ w formie zależności tej energii od gęstości elektronowej. Jest to zatem element teorii funkcjonałów gęstości (DFT). Po wyprowadzeniu równanie uzyskało postać:

    W innych pracach pierwsza całka ma jednak nieco inną postać, którą nazywa się funkcjonałem energii kinetycznej Weizsäckera T_W:

    Różnica polegająca na tym, że we wzorze pierwszym mianownik jest pod kwadratem powoduje kłopoty z całkowaniem. Wystarczy zauważyć, że dla energii stanu podstawowego atomu wodoru znamy ścisły wzór na unormowaną gęstość elektronową w jednostkach atomowych:

   Łatwo się przekonać, że omawiany stosunek z pierwszego równania, będący kwadratem ilorazu gradientu gęstości przez gęstość, musi dać, dla dokładnej postaci równania gęstości, wartość stałą, a to powoduje, że całkowanie, tak zapisanego funkcjonału Weizsäckera, staje się rozbieżne. Należy przyjąć, że kwadrat dotyczy tylko licznika. Poprawiony wzór ma zatem postać:

    Stosunek kwadratu gradientu gęstości elektronowej do gęstości ma postać:

   Pamiętając, że całkowanie odbywa się we współrzędnych sferycznych (jakobian przekształcenia), całkowanie po kątach daje współczynnik 4pi. Przyjmując, że potencjał V_N(r) jest dany wzorem -1/r, ostateczny wzór na energię całkowitą stanu podstawowego atomu wodoru przyjmuje następującą postać:

    

    Wynik jest prawidłowy, gdyż dokładna wartość energii, obliczona dla porównania z równania Schrödingera wynosi dokładnie tyle samo (czyli -1/2) w jednostkach hartree (atomowych).

Literatura: 1. N. H. March, Applications of density functional theory in chemistry, in Density Functional Theory, Ed. E.K.U. Gross and R. M. Dreizler, Plenum Press, New York, 1995 p. 299.

42. Wartości minimalne i maksymalne zmiennej chaotycznej dla kwadratu funcji logarytmicznej w zależności od stałej c

    Ciekawiło mnie, jak zmieniają się wartości minimalne i maksymalne zmiennej chaotycznej x dla szeregu danego wzorem 1.

w zakresie chaotycznym dla stałej c od 0.1 do 1.84. W tym celu napisałem program realizujący to zagadnienie:

'xmin i x max dla obszaru chaotycznego f. log^2

CLS : SCREEN 12

x = .7

testmax = 0

testmin = 100000

OPEN "minmax.txt" FOR APPEND AS #1

FOR c = .1 TO 1.84 STEP .01

 llos = 10000  'liczba iteracji

     'dla c=1.2 min=1.15E-9, max=507.92

 FOR i = 1 TO llos

  x = c * LOG(x) ^ 2  'funkcja logarytmiczna

  IF x >= testmax THEN testmax = x

  IF x <= testmin THEN testmin = x

 NEXT i

 PRINT #1, c, testmin, testmax

NEXT c

    Wyniki przedstawiam w postaci dwóch wykresów ze względu na różnicę wielu rzędów wielkości dla wartości maksymalnej i minimalnej. Pierwszy posiada skalę liniową i pokazuje skokową zmianę wartości maksymalnej przy przechodzeniu od jednej wartości zmiennej c do innej. 

    Drugi wykres ze skalą logarytmiczną eksponuje podobne zmiany dla wartości minimalnej. Kolor niebieski oznacza wartości zmiennej c. Liczby na osi odciętych pokazują numer zmiennej c a nie jej wartość (ot Excel).

    Zmiany te również są skokowe, ale niekoniecznie w tych  samych miejscach, co skoki wartości maksymalnej.