Równanie Schrödingera dla atomu wodoru

Dobór funkcji falowej psi
Wykonanie działania hamiltonianu na funkcję psi
 (patrz dopisek na końcu)
(patrz dopisek na końcu)
 Mnożenie lewostronne
Mnożenie lewostronne


Całkowanie równania

Szukanie minimalnej wartości energii
Na marginesie dodam, że jeśli obliczenia wykonać w jednostkach atomowych, to wówczas stała a przybierze wartość 1/2 oraz b = 1, wówczas c = 1, oraz E = -1/2. Energia podana jest tu w jednostkach hartree.
W celu obliczenia energii atomu wodoru weźmy równanie Schrödingera w przybliżeniu nieruchomego i nieskończenie ciężkiego jądra. Nieruchome jądro pozwala zaniedbać energię kinetyczną protonu. Nieskończenie ciężkie jądro umożliwia pewne uproszczenie obliczeń przez zastosowanie jedynie masy elektronu. Tak skonstruowane równanie ma następującą postać:
Gdzie:
Dodatkowo, operator promienia wodzącego elektronu dany jest wzorem:
W tym: h - stała Plancka (tu podzielona przez 2pi); m - masa elektronu; e - ładunek elementarny; epsilon_zero - stała dielektryczna próżni; r - promień wodzący elektronu.
W celu rozwiązania tego równania należy dobrać funkcję próbną. niech to będzie funkcja eksponencjalna, która posiada element elastyczny, czyli zmienną wariacyjną c:
Działanie to sprowadza się do obliczenia postaci drugich pochodnych funkcji psi po zmiennych x,y,z. Działanie operatora promienia sprowadza się do pomnożenia operatora przez stałe. Do obliczenia drugich pochodnych proponuję zastosować jeden z programów do obliczeń symbolicznych np: Mathcad, Maxima, Mathematica, itp.
Obliczenia prowadzą do następujących wzorów:
Pamiętajmy, że pierwiastek z sumy kwadratów współrzędnych jest promieniem wodzącym elektronu r. Możemy dokonać tej podmiany i zsumować drugie pochodne. W wyniku tego działania i dodania członu operatora energii potencjalnej otrzymuje się następujące wyrażenie:
Wyciągnięcie exp(-cr) przed nawias prowadzi do bardziej zwartego wzoru:
W tym miejscu uzyskane równanie należy pomnożyć lewostronnie przez funkcję sprzężoną do psi. tutaj użyjemy funkcji rzeczywistych, więc funkcja sprzężona jest równa danej funkcji. Proszę zwrócić uwagę, że fakt, czy mnożymy lewo, czy prawostronnie nie ma już znaczenia. Tym niemniej dla zachowania porządku poniższy zapis uwzględnia lewostronność mnożenia:
Po oczywistym wymnożeniu zapis można przedstawić następująco:
Całkowanie równania
Tak uzyskane równanie należy scałkować po całej dziedzinie zmiennych x,x,z.
Tego typu całkę we współrzędnych kartezjańskich trudno jest rozwiązać analitycznie. Wygodnej jest przejść do współrzędnych sferycznych. W tym celu zmienne kartezjańskie należy zastąpić zmiennymi sferycznymi, a równanie pomnożyć obustronnie przez jakobian przekształcenia. Dokonanie tych zmian prowadzi do następującego równania:
Po podstawieniu jakobianu i uporządkowaniu znaków równanie przyjmuje postać:
Całkę potrójną należy przedstawić w postaci iloczynu trzech całek pojedynczych:
Całkowanie po kątach fi i teta daje współczynnik 4π. Wolno zatem ten współczynnik skrócić, gdyż występuje po obu stronach powyższego równania (oznacza to, że rozwiązania są niezależne od kątów, czyli kulistosymetryczne). Pozostaje zatem całkowanie po promieniu wodzącym elektronu. Promień ten rozciąga się od zera do nieskończoności:
Wzór na energię przybiera następującą postać:
Po uporządkowaniu stałych i wyciągnięciu zmiennej r przed nawias, oraz po dokonaniu całkowania otrzymujemy (drugi wzór):
Uproszczenie wyrażenia na energię prowadzi do prostego wzoru, który jest uzależniony od wartości zmiennej c oraz wartości stałych a oraz b oczywiście:
Szukanie minimalnej wartości energii
W celu policzenia energii minimalnej względem c należy obie strony równania zróżniczkować po c:
Stąd już łatwo jest obliczyć wyrażenie na energię minimalną atomu wodoru przez podstawienie wyrażenia na c do równania na energię:
Na marginesie dodam, że jeśli obliczenia wykonać w jednostkach atomowych, to wówczas stała a przybierze wartość 1/2 oraz b = 1, wówczas c = 1, oraz E = -1/2. Energia podana jest tu w jednostkach hartree.
Dopisek. Należy sobie zadać w tym miejscu pytanie, dlaczego nie skraca się obu stron równania przez czynnik exp(-cr). Otóż robi się tak w pewnym sposobie obliczania energii układów kwantowych, który nazywa się metodą energii lokalnych E = Hpsi/psi. Wykorzystuje się tu najczęściej procedurę Monte Carlo z algorytmem Metropolisa. Omówiłem to zagadnienie w innym miejscu.




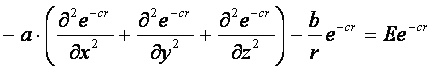













Brak komentarzy :
Prześlij komentarz