Jesteśmy już przygotowani do narysowania prawdziwego orbitalu cząsteczkowego. Dla chemika sprawa to najważniejsza, żeby zrozumieć, co oznacza utworzenie wiązania chemicznego. Tu zajmiemy się stroną matematyczno-graficzną takiego procesu. Na początek warto przygotować rysunek orbitalu wiążącego stanu podstawowego cząsteczki wodoru. Przypominam, iż wszelkie stałe, które należy wprowadzić, aby uzyskać œ ścisły obraz orbitalu cząsteczkowego, zostaną tu pominięte. Nie czas na zajmowanie się tak dokładnymi postaciami funkcji orbitalowych. Na razie najważniejsza jest sama istota, samo sedno matematycznej procedury, która opiera się na dodawaniu (bądź odejmowaniu) orbitali atomowych. W najprostszym wypadku cząsteczki wodoru, wystarczy dodać orbitale 1s atomów wodoru, aby uzyskać zadowalający obraz wiązania sigma. Kluczowym pojęciem pozwalającym tworzyć orbitale cząsteczkowe jest operacja dodawania (lub odejmowania) funkcji orbitalowych. Musimy szczegółowo odpowiedzieć sobie na pytanie, co to znaczy dodać do siebie funkcje typu exp(-r), jeœli jedna z nich znajduje się w początku układu współrzędnych, a druga jest przesunięta na osi x (najlepiej w kierunku wartości dodatnich) o jakąś, chwilowo niezdefiniowaną wielkość. Matematyczna postać takiej sumy jest prosta: exp(-r1) + exp(-r2). Promienie wodzące
r1oraz r2 są związane ze sobą; ich końce wskazują ten sam punkt w przestrzeni. Ponieważ "pracujemy" w przestrzeni dwuwymiarowej, promienie wskazują ten sam punkt na płaszczyźnie xy. Odpowiedni program przedstawiam poniżej.
'----------dane
skala = 50
ustawx = 200
ustawy = 230
kontur = .25
startx = -2
koniecx = 3.5
starty = -5
koniecy = 5
d = 1.5 'odlegloœć między "jšdrami"
boksiatki = .02
a1 = 1: b1 = 1: a2 = 1: b2 = 1: c1 =1: c2 = 2
screen 12
for x = startx to koniecx step boksiatki
for y = starty to koniecy step boksiatki
r1 = sqr(x ^ 2 + y ^ 2)
x2 = d - x
'wzór na r2 wynika z uproszczen geometrycznych.
r2 = sqr(x2 ^ 2 + y ^ 2)
orbital1 = a1*exp(-b1*r1)
orbital2 = a2*exp(-b2*r2)
orbital = c1*orbital1 + c2*orbital2
xekran = x * skala + ustawx
yekran = y * skala + ustawy
if orbital >= kontur then pset (xekran, yekran), 3
if orbital <= -kontur then pset (xekran, yekran), 5
next y
next x
circle (ustawx, ustawy), 4, 4 'jądro1
circle (ustawx + d * skala, ustawy), 4, 6 'jadro2
Poniżej przedstawiłem rysunki orbitalu wiążącego sigma ss i antywiążącego ss, otrzymane za pomocą tego programu.
 |
| Orbital sigma ss wiążący |
 |
| Orbital sigma ss antywiążący |
Analogicznie możemy otrzymać orbital wiążący sigmapp i jego antywiążący odpowiednik, co można uzyskać za pomocą poniższego programu.
'program rysuje przekrój orbitalu molekularnego typu sigma, utworzonego
'przez dwa orbitale typu px.
'---------------
skala = 50
ustawx = 200
ustawy = 230
kontur = .15
startx = -2.7
koniecx = 6
starty = -5
koniecy = 5
dlugosc = 2.5
boksiatki = .02
'----------------
screen 12
for x = startx to koniecx step boksiatki
for y = starty to koniecy step boksiatki
promien1 = sqr(x * x + y * y)
x2 = dlugosc - x
promien2 = sqr(x2 * x2 + y * y)
orbital1 = x * exp(-promien1)
orbital2 = x2 * exp(-promien2)
orbital = .7 * orbital1 + .7 * orbital2
xekran = x * skala + ustawx
yekran = y * skala + ustawy
if orbital >= kontur then pset (xekran, yekran), 3
if orbital <= -kontur then pset (xekran, yekran), 5
next y
next x
circle (ustawx, ustawy), 4, 4
circle (ustawx + dlugosc * skala, ustawy), 4, 6
Poniżej dwa rysunki przedstawiające wynik działania programu dla orbitalu wiążącego i antywiążącego (skala nie jest zachowana).
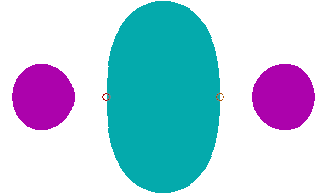 |
| Orbital sigma pp wiążący |
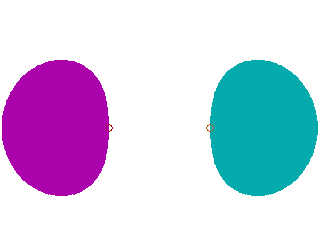 |
| Orbital sigma pp antywiążący |
Na koniec wersja programu, która umożliwia zobrazowanie orbitali pi, utworzonych z dwóch orbitali p
y.
skala = 50
ustawx = 200
ustawy = 230
kontur = .1
startx = -2
koniecx = 4
starty = -5
koniecy = 5
dlugosc = 2
boksiatki = .02
screen 12
for x = startx to koniecx step boksiatki
for y = starty to koniecy step boksiatki
promien1 = sqr(x * x + y * y)
x2 = dlugosc - x
promien2 = sqr(x2 * x2 + y * y)
orbital1 = y * exp(-promien1)
orbital2 = y * exp(-promien2)
orbital = .7 * orbital1 + .7 * orbital2
xekran = x * skala + ustawx
yekran = y * skala + ustawy
if orbital >= kontur then pset (xekran, yekran), 3
if orbital <= -kontur then pset (xekran, yekran), 5
next y
next x
circle (ustawx, ustawy), 4, 4
circle (ustawx + dlugosc * skala, ustawy), 4, 6
W zależności od znaku we wzorze na zmienną orbital otrzymujemy przekrój orbitalu wiążącego lub antywiążącego.
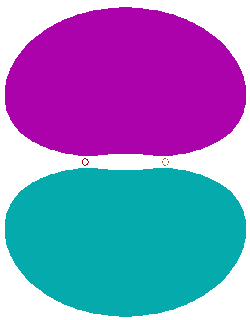 |
| Pi wiążący |
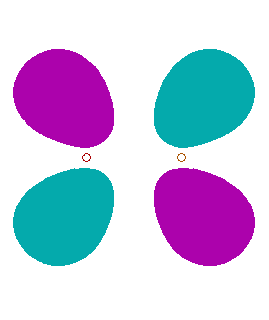 |
| Pi antywiążący |
Przypominam o stałych. Ich właściwe dobranie spowoduje, że funkcje nazywane tu dla uproszczenia orbitalami staną się orbitalami w sensie niemalże ścisłym.



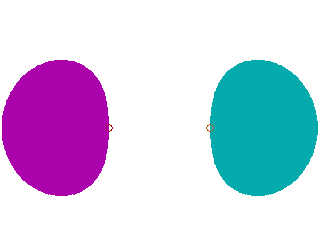
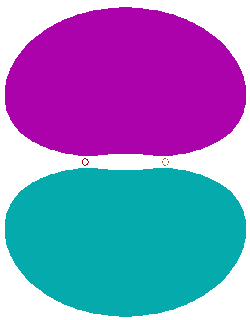

Brak komentarzy :
Prześlij komentarz